评价类模型
层次分析法
1. 概述
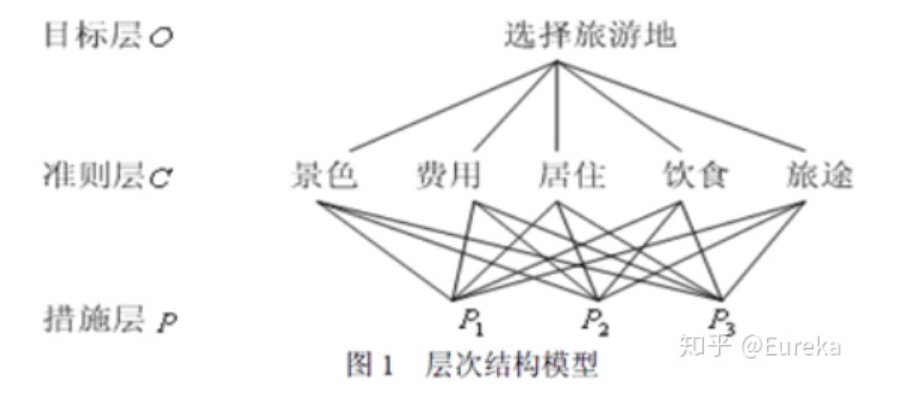
层次分析法(AHP)是将要决策的问题及其有关因素分解成目标、准则、方案等层次,进而进行定性和定量分析的决策方法。它的特征是合理地将定性与定量决策结合起来,按照思维、心理的规律把决策过程细致化(层次化、数量化)。
2. 建模步骤
- 建立递阶层次结构模型;
- 构造出各层次中的所有判断矩阵;
- 层次单排序及一致性检验;
- 层�次总排序及一致性检验。
2.1. 层次建立
2.2. 构建判断矩阵
A=(a11⋮an1...⋱...a1n⋮ann)=(aij)m×n
定义:
定义1: 若矩阵 A=(aij)m×n 满足
- aij>0
- aij=aij1(i,j=1,2,...,n)
称之为正反矩阵。
-
标度

2.3. 层次单排序及一致性检验
一致性矩阵:满足关系式 aijajk=aik,∀i,j,k=1,2,⋯n 的正反矩阵称为一致性矩阵。
-
计算一致性指标CI
CI=n−1λmax−n
-
查找对应的随机一致性指标RI
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|
| RI | 0 | 0 | 0.52 | 0.89 | 1.12 | 1.26 | 1.36 | 1.41 | 1.46 | 1.49 | 1.52 | 1.54 | 1.56 | 1.58 | 1.59 |
-
计算一致性比例CR
CR=RICI
如果CR<0.1,则可以认为判断举证的一致性可以接受;否则需要对判断矩阵镜像修正。
2.4. 判断矩阵计算权重
- 算术平均法求权重
- 几何平均法求权重
- 特征值法求权重
3. 参考文献
1.1 层次分析法模型部分_哔哩哔哩_bilibili
数学建模十大算法之——层次分析法 - 知乎 (zhihu.com)

